The energy of a nucleus can be tapped in two ways: by splitting large nuclei into smaller ones (fission) or by combining small nuclei into larger ones (fusion). The first method yields atomic or nuclear (fission) energy, while the second provides fusion energy, which is essentially stellar power. This is the way the sun and stars generate their energy.
To understand how we can obtain energy from fusing two nuclei, it is essential to know several basic concepts.
- Atomic nuclei are composed of protons and neutrons, each of which has approximately the same mass but a different electric charge.
- When nucleons (a general term for protons and neutrons) are assembled into a nucleus, they are held together by a nuclear force, which is measured by the so-called binding energy. The force of binding energy varies from element to element in the periodic table. For example, the highest binding energy belongs to iron (Fe56), where 56 represents the number of nucleons in its nucleus.
Energy is released when elements are transmuted into other elements that have higher binding energy. Below, you can see a simplified inverted binding energy diagram that illustrates how moving downhill from either side results in the release of energy.
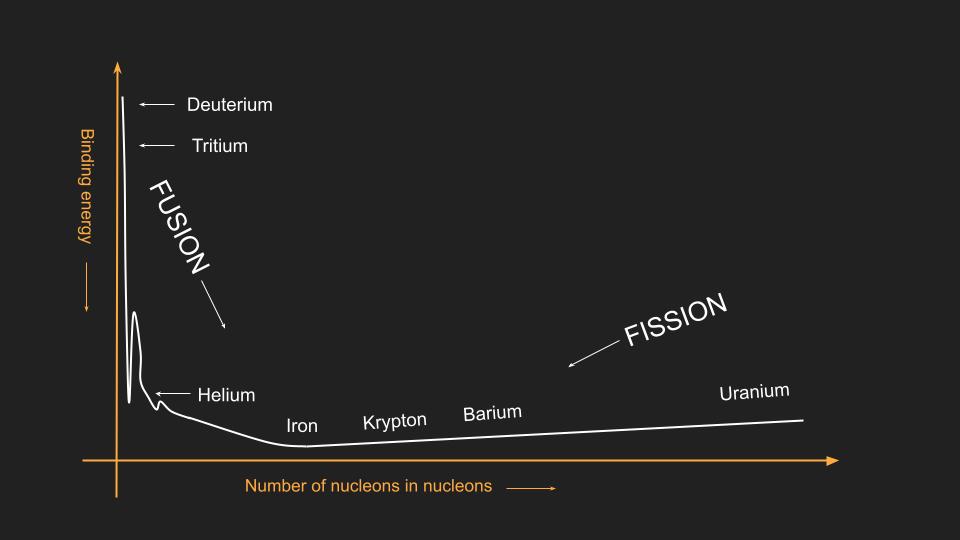
Binding energy is actually inferred from the mass difference. According to Einstein’s equation (E=mc2), energy and mass can be converted into each other. The mass of uranium can be measured to be larger than the sum of the masses of the fission products (barium, Ba144, and krypton, Kr89). Therefore, in the process of splitting uranium, some mass is lost. This lost mass has been converted into energy. Since the velocity of light (c) is a very large number, (c2) is even larger, meaning that a small mass defect can lead to a significant energy output.
mass Uranium > mass Barium + mass Krypton Similarly, in combining deuterium and tritium, the masses of the helium and neutron, produced as a result of the reaction, are smaller than the initial fusion elements.
mass deuterium + mass tritium < mass helium + mass neutronTherefore, mass has been lost, and energy has been gained. Thus, transmuting hydrogen into helium would release a considerable amount of energy. To be more specific, the first step is to use the simplest reaction possible, which is the following:
D + T -> α + n + 17.6 MeV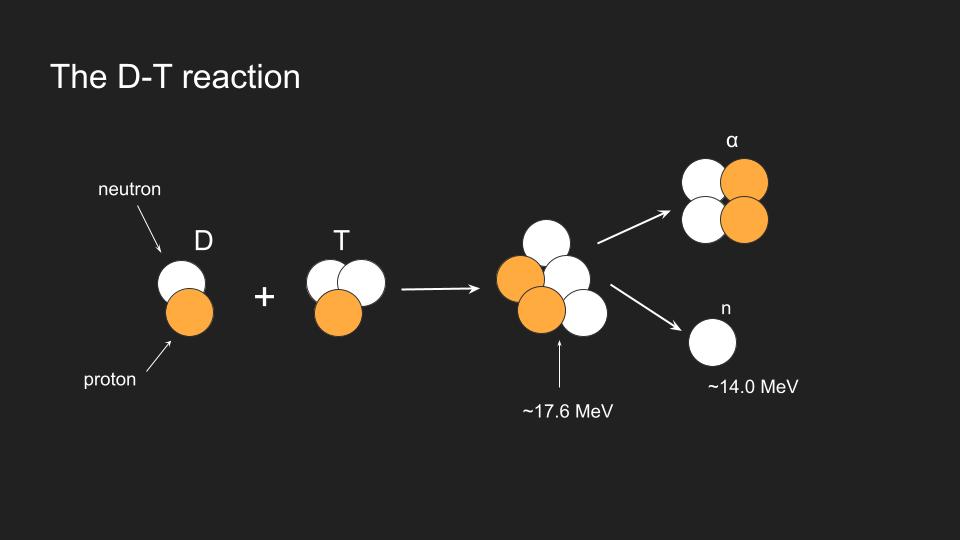
- D – deuterium, is a hydrogen isotope containing 1 proton and 1 neutron
- T – (tritium), containing 1 proton and 2 neutrons
- α – helium nucleus ( He4) with 2 protons and 2 neutrons
- n – is one neutron left over, which flies of carrying most of the energy released in fusion – near 14 MeV
The intermediate state of the reaction is not stable and immediately breaks down into helium and a neutron. The neutron carries approximately 80% of the energy released, and this energy should be converted into heat at a fusion power plant.
Although helium, as a product of the reaction, is not radioactive, the neutron can induce radioactivity in the walls of the reactor, and this material must be properly disposed of, often by burying it.
Nevertheless, radioactive waste from fusion reactions is approximately 1,000 times smaller than that produced by fission nuclear reactors. It is important to note that the deuterium-tritium (D-T) reaction is considered the worst from a radioactivity perspective among fusion reactions. However, it is also the simplest to implement. I will discuss alternative fusion reactions that have reduced or minimal radioactivity in a separate article. A link will be provided here later. If you do not want to miss this publication, please sign up for the newsletter using the form at the end of the current article.
Now, I propose we focus on how we can initiate the deuterium-tritium (D-T) reaction, as it is far from an easy task, and discuss why we need super-hot plasma for this process. However, let’s continue this discussion in another section. I hope to see you soon!
Thank you for your attention, Lumin Hopper


